真の値を我々は知ることができません。測定で得られた結果には必ず不確かさが残ります。
この不確かさを『誤差』と言います。
誤差とは
「誤差 = 測定値 - 真値」で求めることができます。
誤差の分類
誤差は以下の3つに分類ができます。
過誤(過失誤差)
測定者の経験不足や誤操作,記録のミスなど,測定者のミスによって発生する誤差
偶然誤差
測定時の偶然がもたらす誤差。測定器に付着したほこりが原因の誤差。
※測定を繰り返して平均を求めると真の値に近くなる。
系統誤差
特定の原因によって測定値が偏る誤差。測定器の個体差。による誤差。
例えば,定規が曲がっているなど。
※測定を繰り返して平均を求めても真の値に近づかない
※曲がった定規の偏りは一定なのでその誤差は除去できる
系統誤差は以下のものに分類ができます
- 理論誤差
- 固有誤差(測定器などの)
- 個人誤差
- 測定で得られた結果には誤差が含まれる
- 偶然誤差:何度も測定すると誤差が減る
- 統計誤差:何度も測定すると誤差が減らないが,偏り(系統誤差)は除去できる。
誤差の分布
正規分布曲線
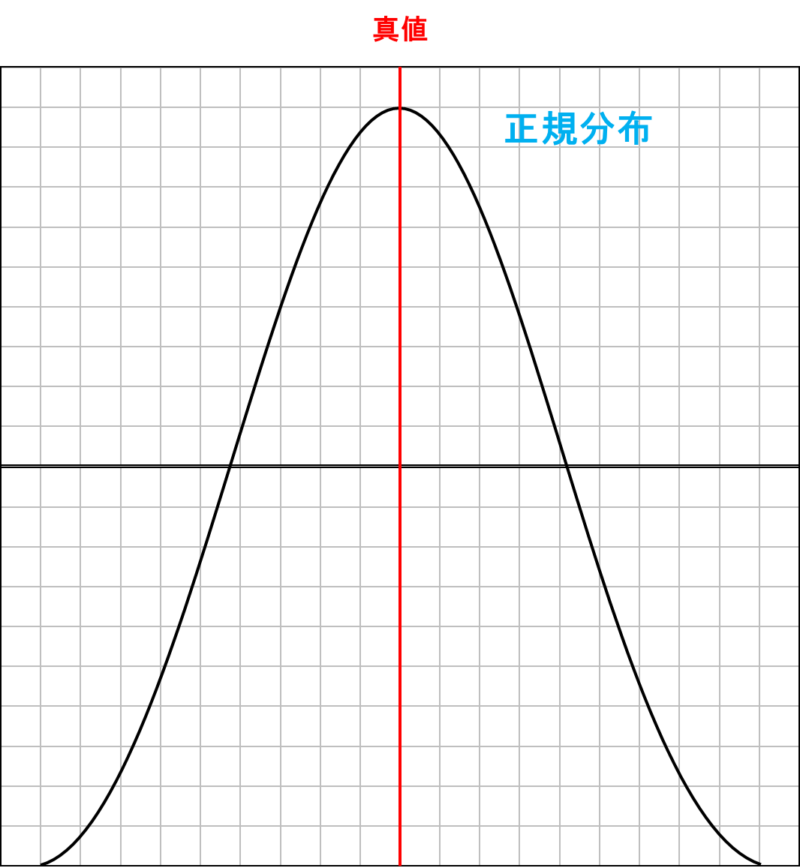
系統誤差,偶然誤差が原因で生じる総合的な誤差の分布は,正規分布曲線で表されることが知られています。
縦軸は度数(出現頻度),横軸が各測定結果を表します。
正規分布曲線は中央値(母平均)が最も高く,離れるに連れて低くなり,また左右対称の形をします。
 onilog
onilog正規分布曲線において「過誤」の誤差は取り除かなければなりません。本質的に正規分布曲線で表される誤差は「系統誤差」「偶然誤差」になります。
正規分布曲線における「かたより」
母平均が真値よりずれている原因は「系統誤差」が原因です。このズレを「かたより」といい,測定器の校正や測定者の訓練教育を行うことで取り除くことのできる誤差と言えます。
かたよりが小さい = 正確さがよい(accuracy)と言います。
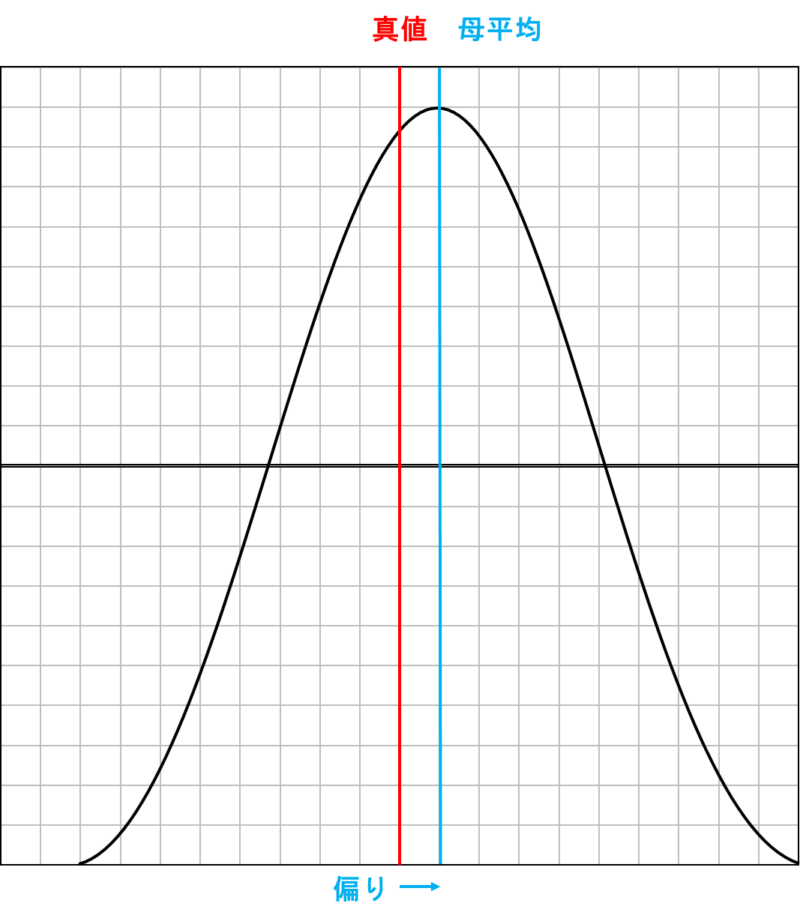




「系統誤差」はある程度取り除くことができますが,完全に取り除くことはできません。
正規分布曲線における「ばらつき」
正規分布曲線から「過誤」「系統誤差」を取り除くことで「偶然誤差」が残ります。偶然誤差は明確に特定することができない誤差のため,基本的に完全に取り除くことができません。このように偶然誤差を正規分布曲線で表すと以下のようになります。
ばらつきが小さい = 精密さがよい(precision)と言います。
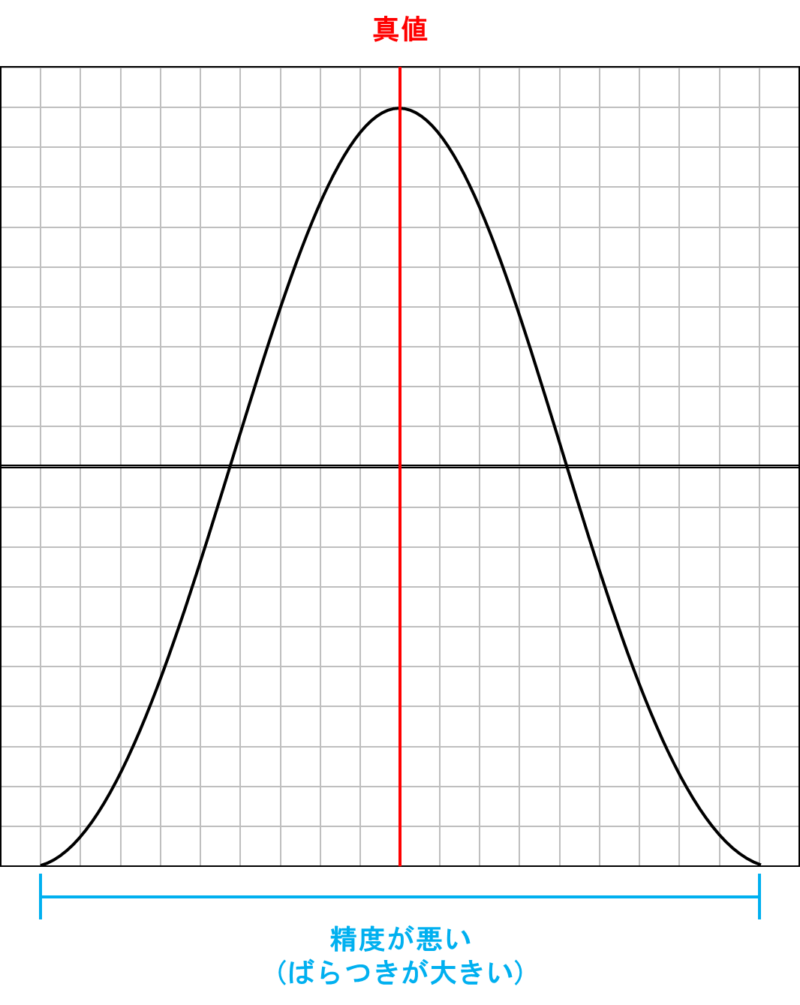

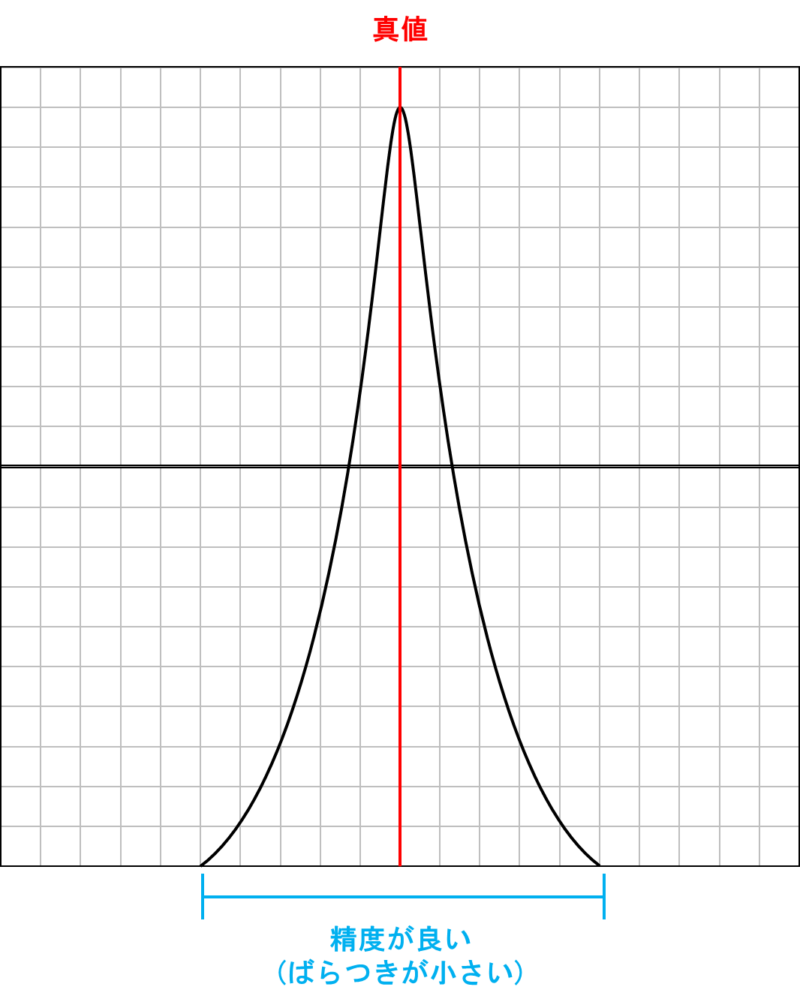




JISでは系統誤差(かたより),偶然誤差(ばらつき)が小さいものほど制度が良いと定義しています。
さいごに
基本的な誤差については以上になりますが,誤差は常に測定において付きまとうものです。
しっかりと理解しておきましょう。
- 真の値は知ることができない
- 誤差を完全に取り除くことはできないが,精度が良い測定(製作)はできる










コメント